Introducción
Entre 1990 y 2023, las exportaciones manufactureras con medio y alto contenido tecnológico de México crecieron significativamente, aunque sin traducirse en una transformación profunda del aparato productivo. El dinamismo exportador, impulsado por la inversión extranjera directa, se concentró en actividades de bajo contenido tecnológico, dominadas por procesos de ensamblaje y una limitada inversión en investigación y desarrollo (I+D). La apertura económica facilitó la integración del país a las cadenas globales de valor, pero también acrecentó su exposición a choques externos. Además, de acuerdo con el Banco Mundial (BM) (2025), la economía mexicana mantiene una alta dependencia a las fluctuaciones del mercado estadounidense, lo que incrementa su vulnerabilidad. En este contexto, México enfrenta el desafío de reorientar su estrategia industrial hacia la producción de bienes manufacturados con mayor complejidad tecnológica y valor agregado (Hausmann et al., 2007; Rodrik, 1998; Romer, 1990).
En consecuencia, el objetivo de la presente investigación es analizar los determinantes de las exportaciones manufactureras de mediana y alta tecnología en México, durante el período 1990-2023. El marco teórico que sustenta el estudio establece que este tipo de exportaciones están influenciadas por factores relacionados con la demanda externa, el precio y costo, la oferta, el capital humano y el nivel educativo, el capital físico, la calidad institucional, aspectos macroeconómicos y otros asociados a contextos específicos (Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Drapkin et al., 2021; 2024; Gómez y Camacho, 2011; Handoyo et al., 2024; Jimenez et al., 2020; Kabaklarli et al., 2017; Karakostas, 2022; Navarro et al., 2024; Ríos et al., 2012).
Con el propósito de alcanzar el objetivo planteado, se estima un Modelo de Corrección de Error Vectorial (VECM) a partir de series de tiempo, el cual permite analizar simultáneamente las relaciones de corto plazo (Cp) y largo plazo (Lp) entre variables macroeconómicas no estacionarias y cointegradas (Lütkepohl y Krätzig, 2004). Siendo, la variable dependiente las exportaciones manufactureras de mediana y alta tecnología (XMAT) y las variables independientes las XMAT de un periodo anterior (XMAT-1), el gasto en investigación y desarrollo (GIYD), la inversión extranjera directa (IED), el grado de apertura comercial de la economía mexicana (IAC) y por la demanda de Estados Unidos (PIB_USA). La información estadística proviene del Banco Mundial (2025) y las estimaciones se realizan con el paquete estadístico Eviews.
El documento se estructuró en seis apartados, comenzando con la introducción, continuando con el análisis de la dinámica de los indicadores macroeconómicos relacionados con las XMAT, en el tercer apartado se presentan los aspectos teóricos de los determinantes de las XMAT, en el cuarto se detallan los aspectos metodológicos del modelo VECM, en el quinto se muestran y discuten los resultados del modelo econométrico, y finalmente se establecen una serie de conclusiones.
Dinámica de las exportaciones manufactureras de mediana y alta tecnología
El desempeño de las XMAT constituye un eje central para evaluar la transformación económica de México en las últimas décadas. Entre 1990 y 2023, estas exportaciones experimentaron un crecimiento significativo, al pasar de 18,025 millones de dólares en 1990 a 256,264 millones de dólares en 2023. Este comportamiento ha estado condicionado por la dinámica e interacción de diversos factores macroeconómicos (Banco Mundial, 2025).
La evolución del Producto Interno Bruto (PIB) de México, con una tasa de crecimiento del 194% y una media de 955,181 millones de dólares, refleja una expansión económica moderada. Esta trayectoria estuvo condicionada por los ciclos económicos globales, las crisis internas y las distintas reformas estructurales, cuyo impacto sobre el aparato productivo fue heterogéneo. Aunque el crecimiento económico favoreció la expansión de las exportaciones, no promovió una transformación integral de las capacidades productivas del país, como lo demuestra la persistente concentración de la producción de manufacturas de tecnología media (Banco Mundial, 2025).
El comercio exterior desempeñó un papel fundamental en este proceso. Las exportaciones totales de bienes y servicios crecieron a una tasa del 525%, mientras que las importaciones lo hicieron en 622%, favoreciendo una mayor inserción de México en las cadenas globales de valor, especialmente tras la entrada en vigor del TLCAN. En este contexto, las exportaciones manufactureras pasaron de tener un peso moderado a convertirse en el motor principal de las ventas externas, con un aumento del 1027% en el período de estudio. Destaca el incremento de las exportaciones manufactureras de media y alta tecnología, que crecieron en un 1336%; no obstante, la participación de las manufacturas de tecnología media es mayor que las de alta tecnología (Banco Mundial, 2025).
El índice de apertura comercial (IAC) revela una creciente internacionalización de la economía mexicana, al pasar de 33.3% en 1990 a 72% en 2023, lo que representa un aumento del 116%. No obstante, el IAC presentó retrocesos en periodos de crisis o de reestructuración interna, como ocurrió en 1993, cuando el índice cayó a 22% (Rodrik, 1998). Si bien la apertura impulsó las exportaciones, también elevó la exposición a choques externos. En este marco, la inversión extranjera directa desempeñó un rol estratégico, al pasar de 4,395 millones de dólares en 1990 a 21,622 millones de dólares en 2023 (Banco Mundial, 2025). Dicha inversión se concentró en sectores manufactureros como el automotriz, el electrónico y el de maquinaria, lo que potenció las XMAT; sin embargo, se dio bajo un esquema centrado en el ensamblaje, con escaso desarrollo de capacidades tecnológicas propias (Lall, 2000).
En cuanto al capital humano, México ha registrado avances importantes, aunque aún insuficientes. El promedio de años de educación superior de la población mayor de 25 años pasó de 0.27 en 1990 a 0.92 en 2023. A su vez, la escolaridad total de mayores de 15 años alcanzó 9.61 años en 2023, reflejando un incremento del 48% en el período analizado (Banco Mundial, 2025). Pese a estos progresos, el país continúa rezagado respecto a economías líderes en innovación, lo que limita su capacidad para consolidar sectores de alta tecnología (Romer, 1990). Por su parte, el gasto en I+D aumentó un 777%, ya que pasó de 640 millones de dólares en 1990 a 3,260 millones de dólares en 2023. Sin embargo, este sigue siendo insuficiente para promover la innovación endógena, lo que ha generado una alta dependencia de la importación de bienes de tecnología de la información y la comunicación (TIC), que alcanzaron un promedio anual de 40,297 millones de dólares y registraron un incremento del 1046% entre 1990 y 2023 (Banco Mundial, 2025).
El entorno financiero en México presentó condiciones mixtas. Las tasas de interés reales fueron altamente volátiles, con episodios negativos durante la década de 1990, reflejando inestabilidad macroeconómica. A su vez, las tasas de interés de los préstamos se mantuvieron elevadas, con un promedio del 13%, restringiendo el acceso al crédito productivo, especialmente para las micro, pequeñas y medianas empresas fuera de los conglomerados exportadores. En contraste, el contexto internacional fue más favorable. Entre 1990 y 2023, el PIB de Estados Unidos creció un 99%, generando una demanda externa sólida para las exportaciones mexicanas y fortaleciendo su desempeño. No obstante, esta dinámica también consolidó una dependencia cíclica de México respecto a la economía estadounidense (Banco Mundial, 2025; Frieden, 2007; Reinhart y Rogoff, 2009).
Análisis teórico de los determinantes de las exportaciones manufactureras de mediana y alta tecnología
Las exportaciones, y en particular las manufactureras, han sido reconocidas durante mucho tiempo como un pilar fundamental para el crecimiento económico y la mejora de la competitividad nacional (Fayaz y Kaur, 2019; Gómez y Camacho, 2011; Jimenez et al., 2020). En el contexto económico actual, la sofisticación tecnológica de las exportaciones manufactureras adquiere una relevancia estratégica (Navarro et al., 2024).
Los modelos teóricos tradicionales de exportación han privilegiado los factores de demanda y precio, estableciendo una relación positiva entre las exportaciones y el ingreso de los socios comerciales, y negativa respecto al precio relativo de los bienes exportados. Sin embargo, la evidencia empírica ha demostrado que omitir factores de oferta puede sesgar las estimaciones. En consecuencia, la literatura reciente sostiene que las exportaciones dependen no solo del tipo de cambio real y la demanda externa, sino también de la demanda interna y de variables asociadas a la oferta. Esta perspectiva que retoma los factores de demanda y oferta ha dado origen a los denominados modelos híbridos o funciones ampliadas de exportación (Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Fayaz y Kaur, 2019; Jimenez et al., 2020; Navarro et al., 2024; Ríos et al., 2012). Lo cual es especialmente relevante en el caso de las exportaciones manufactureras de bienes con medio y alto contenido tecnológico.
En este sentido, las investigaciones empíricas que emplean modelos econométricos han identificado diversos determinantes clave de las exportaciones manufactureras, los cuales pueden agruparse en las siguientes categorías:
- Factores de demanda externa. La demanda externa constituye un elemento decisivo de las exportaciones manufactureras, dado que su crecimiento incide directamente en el volumen exportado. Comúnmente, se estima mediante indicadores como el PIB o las importaciones totales de los principales socios comerciales. En el caso de México, su alta dependencia de la economía estadounidense resalta la relevancia de este factor (Anh et al., 2023; Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Gómez y Camacho, 2011; Shahabadi et al., 2023).
- Factores de precio y costo. El tipo de cambio real presenta efectos ambiguos sobre las exportaciones manufactureras. La evidencia para México indica que su depreciación puede generar impactos negativos en el Cp y que no constituye un determinante significativo, posiblemente debido al alto grado de integración productiva con Estados Unidos. En contraste, los costos laborales unitarios sí muestran una incidencia significativa sobre las exportaciones. Su reducción, particularmente cuando obedece a incrementos en la productividad, tiende a favorecer las exportaciones manufactureras, especialmente en sectores con menor contenido tecnológico (Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Gómez y Camacho, 2011).
- Factores de oferta. La productividad laboral impulsa las exportaciones manufactureras al reducir costos y elevar la calidad, siendo más eficaz que la depreciación cambiaria. En productos de mediana y alta tecnología, la innovación y el desarrollo tecnológico es un determinante clave, medido por el gasto en I+D, el número de patentes y la importación de bienes tecnológicos. Asimismo, la estructura de mercado, la diferenciación de productos y la capacidad instalada utilizada inciden significativamente en el desempeño exportador (Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Drapkin et al., 2024; Fayaz y Kaur, 2019; Gómez y Camacho, 2011; Jimenez et al., 2020; Kabaklarli et al., 2017; Karakostas, 2022; Navarro et al., 2024).
- Factores de capital humano y educativos. El capital humano, medido por el nivel educativo, es un elemento fundamental para las exportaciones de alta tecnología, ya que facilita la adopción de tecnologías avanzadas, promueve la innovación y aumenta la eficiencia, la productividad y la competitividad. En América Latina y México, la falta de capital humano limita el desarrollo de sectores tecnológicos, lo que hace necesario invertir en educación de calidad y formación profesional (Anh et al., 2023; Cuevas-Ahumada y Jaime, 2024; Drapkin et al., 2024; Gómez y Camacho, 2011; Jimenez et al., 2020; Navarro et al., 2024; Tebaldi, 2011).
- Factores de capital. La inversión extranjera directa puede desempeñar un papel relevante en el impulso de las exportaciones, especialmente aquellas con alto contenido tecnológico, al facilitar la adopción de tecnologías avanzadas y prácticas de gestión más eficientes. Aunque la evidencia empírica muestra resultados heterogéneos. Por otra parte, otros indicadores de inversión, como la formación bruta de capital, también han sido vinculados positivamente con las exportaciones tecnológicas (Cuevas-Ahumada, 2011; Drapkin et al., 2024; Fonkam, 2023; Jimenez et al., 2020; Kabaklarli et al., 2017; Leogrande et al., 2022; Navarro et al., 2024; Shahabadi et al., 2023).
- Factores institucionales y macroeconómicos: La calidad de la gobernanza y el entorno institucional desempeñan un papel importante en el desarrollo de las exportaciones de mediana y alta tecnología. Elementos como una regulación gubernamental eficiente, estabilidad política, control de la corrupción, flexibilidad administrativa y protección de la propiedad intelectual contribuyen a su expansión. En contraste, condiciones macroeconómicas adversas -políticas fiscales restrictivas, altas tasas de inflación, desempleo y una elevada carga impositiva- pueden limitar su crecimiento. Asimismo, mientras que la deuda externa puede tener efectos positivos en ciertos contextos, la abundancia de recursos naturales suele impactar negativamente las exportaciones tecnológicas (Drapkin et al., 2024; Navarro et al., 2024).
- Otros factores de tipo contextual: Variables relacionadas con contextos específicos, como las medidas adoptadas durante la pandemia del covid-19, también han demostrado ser relevantes. Un mayor nivel de rigurosidad en las medidas de distanciamiento social reduce las exportaciones manufactureras, mientras que una mayor cobertura de vacunación las estimula. Estos resultados subrayan la importancia de coordinar las políticas económicas y de salud para mitigar los efectos negativos sobre el comercio exterior (Anh et al., 2023; Cuevas-Ahumada y Jaime, 2024).
Aspectos metodológicos del modelo de corrección de error vectorial
Especificaciones teórico–metodológicas del modelo VECM
El análisis econométrico de series de tiempo ha experimentado importantes avances desde la introducción de los modelos ARIMA de Box y Jenkins (1970), promoviendo una integración entre técnicas estadísticas y teoría económica (Box et al., 2015; Palm, 1986). Ello es consecuencia del hecho de que muchas variables macroeconómicas son no estacionarias, lo que infringe los supuestos clásicos de los modelos de regresión (Shrestha y Bhatta, 2018). Granger y Newnegritas (1974) advirtieron que el uso de este tipo de series genera relaciones espurias, lo que llevó al desarrollo de las pruebas de raíz unitaria y las técnicas de cointegración, capaces de identificar relaciones estables de Lp entre variables no estacionarias (Engle y Granger, 1987). Johansen (1988, 1991) amplió este enfoque mediante el método de máxima verosimilitud para estimar múltiples vectores de cointegración. A partir de ello, se consolidó el Modelo de Corrección de Error Vectorial (VECM), que integra la dinámica de Cp de los modelos de Vector Autorregresivo (VAR) con restricciones de equilibrio de Lp derivadas de la cointegración (Shrestha y Bhatta, 2018; White, 1980).
La construcción de un VECM comienza con el análisis exploratorio de las series de tiempo, a fin de identificar tendencias, estacionalidades, ciclos, valores atípicos o cambios estructurales (Shrestha y Bhatta, 2018). Ello se complementa con el cálculo de estadísticos descriptivos y el análisis de las funciones de autocorrelación y autocorrelación parcial, que permiten evaluar la dependencia temporal, detectar la posible presencia de raíces unitarias, y distinguir entre tendencias deterministas o estocásticas en las series (Gujarati, 2014). A partir de este diagnóstico inicial, se aplican transformaciones logarítmicas o de diferenciación y se formulan hipótesis sobre el orden de integración de las series (Martin et al., 2013; Studenmund, 2017; Wooldridge, 2019).
En una segunda etapa, se aplican pruebas de raíz unitaria con el fin de determinar formalmente el orden de integración de las series y verificar la presencia de no estacionariedad. La estacionariedad implica que la media, la varianza y las covarianzas son constantes en el tiempo; su ausencia puede invalidar los supuestos del modelo de regresión y conducir a inferencias erróneas (Granger y Newnegritas, 1974; Gujarati, 2014). La prueba más utilizada es la Dickey-Fuller Aumentada (ADF), la cual establece que, si el coeficiente de resulta significativamente negativo, se rechaza la hipótesis nula de no estacionariedad y se concluye que la serie es estacionaria; de lo contrario, se clasifica como integrada de orden uno (I(1)) (Dickey y Fuller, 1981). La prueba Phillips-Perron (PP), que llega a resultados similares que la ADF, ajusta los errores estándar para corregir la autocorrelación y la heterocedasticidad, sin necesidad de incluir rezagos adicionales (Phillips y Perron, 1988). Ambas pruebas suelen complementarse con la prueba KPSS, que ofrece una perspectiva contrastante al establecer la estacionariedad como hipótesis nula (Greene, 2019; Kwiatkowski et al., 1992). Ante la posible presencia de cambio estructural en una serie, se aplican versiones modificadas de estas pruebas, que consideran dichos quiebres a fin de evitar interpretaciones erróneas (Perron, 1989; Zivot y Andrews, 1992; Studenmund, 2017).
El siguiente paso en la construcción del modelo VECM es la selección del número óptimo de rezagos (p), decisión fundamental para garantizar la validez del modelo. Un número insuficiente de rezagos puede provocar autocorrelación residual, mientras que una cantidad excesiva de ellos ocasiona sobreparametrización y pérdida de eficiencia (Lütkepohl y Krätzig, 2004). Para orientar esta elección, se utilizan criterios de información como el de Akaike (AIC), el de Schwarz o de Bayes (BIC/SBC) y el de Hannan-Quinn (HQ). El AIC favorece modelos más complejos, el BIC prioriza la simplicidad y el HQ ofrece un punto intermedio. Se selecciona el valor de p que minimiza el criterio correspondiente, y su validez debe comprobarse con pruebas de autocorrelación, como Ljung-Box o LM de Breusch-Godfrey, considerando también la frecuencia de los datos y el tamaño muestral (Wooldridge, 2019).
Cuando varias series de tiempo son I(1), pueden existir entre ellas una o más combinaciones lineales que sean estacionarias, lo que indica la presencia de cointegración (Engle y Granger, 1987). Esto implica una relación de equilibrio de Lp, en la que las variables, aunque se desvíen en el Cp, tienden a moverse juntas en el Lp. El método Engle-Granger, adecuado para sistemas bivariados, estima una regresión a nivel y evalúa la estacionariedad de los residuos, si estos son estacionarios, se establece que existe cointegración. No obstante, sus limitaciones lo hacen inapropiado para contextos multivariados (Shrestha y Bhatta, 2018; Townsend, 1998). En estos casos, el enfoque de Johansen (1988, 1991) es más robusto, ya que reformula el VAR como un VECM e identifica el número de vectores de cointegración mediante pruebas de traza y máximo autovalor, estimando de forma simultánea los vectores de cointegración (β) y las velocidades de ajuste (α) en un marco de máxima verosimilitud. Alternativamente, el enfoque ARDL permite evaluar cointegración incluso con variables mixtas (I(0) e I(1)) (Pesaran et al., 2001).
Confirmado el orden de integración I(1) de las series y la existencia de cointegración, se justifica la especificación del modelo VECM. Este modelo representa una reformulación del VAR que incorpora explícitamente los equilibrios de Lp, combinando dos componentes: la dinámica de Cp, capturada por las primeras diferencias de las variables, y los términos de corrección de error, que reflejan los desajustes respecto al equilibrio. La forma general de un VECM es (Lütkepohl y Krätzig, 2004):
Donde es el vector de variables endógenas en nivel, representa sus primeras diferencias, son matrices de coeficientes que capturan la dinámica de Cp, es un vector de constantes, y es el vector de errores aleatorios. Si existe cointegración, la matriz tiene rango reducido y se factoriza como , donde contiene los vectores de cointegración y las velocidades de ajuste hacia el equilibrio.
Los parámetros del modelo se estiman mediante el método de máxima verosimilitud propuesto por Johansen (1988, 1991), lo que permite estimar simultáneamente y . La significatividad de indica qué variables reaccionan a los desequilibrios de Lp, mientras que las matrices explican efectos dinámicos de Cp. Además, es posible imponer restricciones teóricas sobre , cuya validez puede evaluarse mediante pruebas de razón de verosimilitud, lo que contribuye a garantizar la coherencia del modelo. Es así como, el VECM permite modelar de forma conjunta las relaciones de Cp y Lp entre variables cointegradas (Lütkepohl y Krätzig, 2004).
Una vez estimado el modelo VECM, su validación es fundamental para garantizar la confiabilidad de los resultados e inferencias. Esta etapa implica una serie de pruebas diagnósticas esenciales (Studenmund, 2017). Primero, se debe comprobar que los residuos no presenten autocorrelación mediante pruebas como Ljung-Box o LM de Breusch-Godfrey; si se detecta autocorrelación, el modelo debe reespecificarse. Segundo, se evalúa la homocedasticidad con las pruebas de White (1980) o Breusch-Pagan (1979); ante heterocedasticidad, se sugiere el uso de errores robustos o modelos alternativos como GARCH. Tercero, la normalidad de los residuos se verifica con la prueba de Jarque-Bera o Doornik-Hansen, siendo necesarias adecuaciones en el modelo si esta condición no se cumple (Jarque & Bera, 1987). Cuarto, se analiza la estabilidad del modelo mediante la verificación de raíces características, pruebas CUSUM y Chow; su incumplimiento compromete la validez de las inferencias, exigiendo ajustes estructurales o segmentación temporal. Quinto, se evalúa la capacidad predictiva del modelo a través de ejercicios de validación fuera de la muestra, empleando métricas como el RMSE (Root Mean Squared Error), MAE (Mean Absolute Error) o Theil U; errores sistemáticos o un mal desempeño cuestionan su utilidad predictiva (Lütkepohl y Krätzig, 2004; Shrestha y Bhatta, 2018).
Una vez estimado y validado el modelo VECM, el análisis final se centra en la interpretación económica de sus resultados. Los reflejan relaciones de equilibrio de Lp entre las variables, y su interpretación requiere sustento teórico (Gujarati, 2014; Wooldridge, 2019). Los indican qué variables responden a los desequilibrios y con qué intensidad, permitiendo diferenciar entre variables endógenas y exógenas en el Lp. El VECM permite también análisis dinámicos mediante funciones de impulso-respuesta (IRF) y de descomposición de la varianza del error de pronóstico (FEVD). Las IRF permiten observar la relación temporal de las variables ante shocks y su proceso de ajuste hacia nuevos equilibrios. La FEVD, por su parte, cuantifica la contribución de cada shock a la varianza de las variables en distintos horizontes (Lütkepohl y Krätzig, 2004).
Variables del modelo VECM
A fin de identificar los determinantes de las exportaciones manufactureras de mediana y alta tecnología en México durante el período 1990-2023, se realizó un análisis exhaustivo de la literatura y se contrastaron las bases estadísticas internacionales para verificar la disponibilidad de los datos. A raíz de ello, las variables seleccionadas para estimar el modelo fueron las siguientes: a) la variable dependiente son las exportaciones manufactureras con medio y alto contenido tecnológico; y las variables independientes fueron el gasto en investigación y desarrollo, la inversión extranjera directa, el índice de apertura comercial, y el PIB de los Estados Unidos (véase Tabla 1). Para evitar las fluctuaciones bruscas en los datos y la heterogeneidad de las series temporales, todas las variables se convierten en logaritmos naturales (ln). Por otro lado, el software que se utiliza para estimar el modelo econométrico es Eviews.
Tabla 1. Descripción de las variables
| Variable | Definición | Unidad de Medida | Estudios previos | Nomenclatura | Fuente |
|---|---|---|---|---|---|
| Exportaciones Manufactureras de Media y Alta Tecnología | Volumen de exportaciones manufactureras con medio y alto contenido tecnológico | Dólares americanos constantes de 2010. | Drapkin et al., 2021, 2024; Fayaz y Kaur, 2019; Güneş et al., 2020; Handoyo et al., 2024; Jimenez et al., 2020; Kabaklarli et al., 2017; Karakostas, 2022; Leogrande et al., 2022; Navarro et al., 2024; Tebaldi, 2011. | XMAT | Banco Mundial (2025). |
| Gasto en Investigación y Desarrollo | Nivel de gasto en investigación y desarrollo en el país | Dólares americanos constantes de 2010. | Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Drapkin et al., 2024; Fayaz y Kaur, 2019; Gómez y Camacho, 2011; Jimenez et al., 2020; Kabaklarli et al., 2017; Karakostas, 2022; Navarro et al., 2024. | GIYD | Banco Mundial (2025). |
| Inversión Extranjera Directa | Flujos de inversión extranjera directa al país | Dólares americanos constantes de 2010. | Cuevas-Ahumada, 2011; Drapkin et al., 2024; Fonkam, 2023; Jimenez et al., 2020; Kabaklarli et al., 2017; Leogrande et al., 2022; Navarro et al., 2024; Shahabadi et al., 2023. | IED | Banco Mundial (2025). |
| Índice de Apertura Comercial | Grado de apertura comercial del país | Índice | Anh et al., 2023; Cuevas-Ahumada, 2011; Cuevas-Ahumada & Jaime, 2024; Drapkin et al., 2024; Gómez y Camacho, 2011; Navarro et al., 2024; Ríos et al., 2012; Shahabadi et al., 2023. | IAC | Banco Mundial (2025). |
| PIB de los Estados Unidos | Demanda externa | Dólares americanos constantes de 2010. | Cuevas-Ahumada, 2011; Cuevas-Ahumada & Jaime, 2024; Gómez y Camacho, 2011. | PIB_USA | Banco Mundial (2025). |
Fuente: Elaboración propia.
A partir de ello, y con la intención de apreciar la incidencia de Cp y Lp del gasto en investigación y desarrollo, la inversión extranjera directa, el índice de apertura comercial, y el PIB de los Estados Unidos en las exportaciones manufactureras de media y alta tecnología de México, en el período 1990-2023, se estima la ecuación 1.
Resultados y discusión del modelo
Análisis de los resultados del modelo VECM
Tabla 2. Estadísticas descriptivas
| Estadístico | XMAT | GIYD | IED | IAC | PIB_USA |
|---|---|---|---|---|---|
| Media | 152,207,021,937 | 3,306,609,367 | 23,472,898,014 | 0.54 | 14,484,270,261,235 |
| Mediana | 147,643,461,485 | 3,301,828,298 | 24,187,441,025 | 0.50 | 14,829,702,209,090 |
| Máximo | 258,814,781,230 | 5,614,963,099 | 47,669,773,159 | 0.89 | 19,837,944,375,684 |
| Mínimo | 18,025,887,472 | 640,088,852 | 4,395,878,719 | 0.22 | 9,859,736,142,638 |
| Desviación Estándar | 74,466,688,856 | 1,439,147,226 | 9,606,102,376 | 0.18 | 2,916,227,813,541 |
| Asimetría | -0.19 | -0.14 | -0.05 | 0.30 | 0.06 |
| Curtosis | 1.90 | 2.10 | 2.98 | 2.18 | 2.00 |
| Jarque-Bera | 1.92 | 1.26 | 0.01 | 1.45 | 1.42 |
| p-valor | 0.38 | 0.53 | 0.99 | 0.48 | 0.49 |
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
El análisis exploratorio de las variables indica que la media de estas es positiva, que los valores de la media y la mediana son muy similares, y que el p-valor de las pruebas de Jarque-Bera son superiores al 0.05. Todo ello sugiere que las variables empleadas en el modelo poseen una distribución normal (véase Tabla 2).
La matriz de correlaciones ofrece una primera aproximación a la relación entre las XMAT y sus determinantes. En la Tabla 3 se observa que todas las variables explicativas presentan una correlación positiva con las XMAT, destacando el PIB_USA como la variable con mayor correlación, con un valor de 0.978. Le sigue el IAC, la IED y el GIYD, con coeficientes de 0.947, 0.729 y 0.653, respectivamente. Ello evidencia una relación positiva y significativa entre dichas variables y las exportaciones manufactureras de mediana y alta tecnología en México durante el período 1990-2023.
Tabla 3. Matriz de correlación
| XMAT | GIYD | IED | IAC | PIB_USA | |
|---|---|---|---|---|---|
| XMAT | 1 | 0.653 | 0.729 | 0.947 | 0.978 |
| GIYD | 0.653 | 1 | 0.717 | 0.459 | 0.584 |
| IED | 0.729 | 0.717 | 1 | 0.628 | 0.680 |
| IAC | 0.947 | 0.459 | 0.628 | 1 | 0.957 |
| PIB_USA | 0.978 | 0.584 | 0.680 | 0.957 | 1 |
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
La prueba de raíces unitarias aplicada a las variables consideradas en el modelo, mediante la prueba ADF, indica que todas ellas son integradas de orden uno o I(1), es decir, presentan estacionariedad en primeras diferencias (véase Tabla 4).
Tabla 4. Prueba Dickey-Fuller Ampliada
| Variable | Sin diferenciar | Primera diferencia |
|---|---|---|
| p-valor | p-valor | |
| lnXMAT | 0.0001 | 0.0027 |
| lnGIYD | 0.0084 | 0.0269 |
| lnIED | 0.0027 | 0.0000 |
| lnIAC | 0.7241 | 0.0003 |
| lnPIB_USA | 0.8572 | 0.0001 |
|
Nota: Si el p > 0.05, se dice que tiene raíz unitaria o que es no estacionaria. |
||
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
A continuación, se presentan los resultados correspondientes a la determinación del número óptimo de rezagos. Para ello, se emplearon distintos criterios de información: la LR secuencial modificada (LR), el error de predicción final (FPE), el Akaike (AIC), el de Schwarz (SBC) y el de Hannan-Quinn (HQ). Como se puede apreciar en la Tabla 5, la mayoría de los criterios coinciden en señalar el tercer rezago como el más adecuado, al registrar los valores mínimos. En consecuencia, se decide incorporar tres rezagos en la estimación de la prueba de cointegración.
Tabla 5. Selección de la cantidad óptima de rezagos
| Rezago | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|
| 0 | NA | 5.70e+15 | 50.46884 | 50.70238* | 50.54355* |
| 1 | 24.61844 | 1.11e+16 | 51.10974 | 52.51094 | 51.55800 |
| 2 | 38.27286 | 9.14e+15 | 50.76205 | 53.33091 | 51.58385 |
| 3 | 39.48750* | 4.46e+15* | 49.60818* | 53.34470 | 50.80352 |
| Nota: * indica el orden de rezago seleccionado por el criterio. | |||||
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
La prueba de Johansen evidencia la existencia de un máximo de tres vectores de cointegración. En ese sentido, se establece que el modelo presenta al menos tres posibles relaciones de cointegración entre las variables analizadas (véase Tabla 6).
Tabla 6. Pruebas de cointegración de Johansen
| Cantidad de vectores de cointegración | Prueba de traza | Prueba de valor propio máximo | ||
|---|---|---|---|---|
| Estadístico | p-valor | Estadístico | p-valor | |
| Ninguno * | 124.5140861 | 0.00000 | 48.71769 | 0.00000 |
| Máximo 1 * | 75.79639679 | 0.00002 | 41.62348 | 0.00002 |
| Máximo 2 * | 34.17291839 | 0.01471 | 21.79125 | 0.01471 |
| Máximo 3 | 12.38166387 | 0.13953 | 11.73914 | 0.13953 |
| Máximo 4 | 0.642527257 | 0.42280 | 0.64253 | 0.42280 |
|
Nota: * indica el rechazo de la hipótesis nula a un p-valor de 0.05. |
||||
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
Una vez confirmado que las series son integradas de orden uno y que existe cointegración entre ellas, se estima el modelo VECM. Los resultados de este manifiestan, en primer lugar, la existencia de una relación de causalidad de Lp entre el conjunto de variables independientes (lnXMAT-1, lnGIYD, lnIED, lnIAC y lnPIB_USA) y la variable dependiente (lnXMAT). En este sentido, se puede apreciar en la Tabla 7 que el coeficiente de los elementos de corrección de error (C(1)) resulta estadísticamente significativo. Por lo tanto, se puede señalar que las variables explicativas del modelo mantienen una relación de equilibrio de Lp con la variable dependiente.
Tabla 7. Resultados del modelo VECM
| Ecuación guía del modelo: | ||||||
|---|---|---|---|---|---|---|
|
D(L_XMAT) = C(1)*( L_XMAT(-1) - 8.63861117569*L_GIYD(-1) + 21.0336771887*L_IED(-1) - 11.9646038859*L_IAC(-1) + 20.2106821091*L_PIB_USA(-1) - 959.065594081 ) + C(2)*D(L_XMAT(-1)) + C(3)*D(L_XMAT(-2)) + C(4)*D(L_XMAT(-3)) + C(5)*D(L_GIYD(-1)) + C(6)*D(L_GIYD(-2)) + C(7)*D(L_GIYD(-3)) + C(8)*D(L_IED(-1)) + C(9)*D(L_IED(-2)) + C(10)*D(L_IED(-3)) + C(11)*D(L_IAC(-1)) + C(12)*D(L_IAC(-2)) + C(13)*D(L_IAC(-3)) + C(14)*D(L_PIB_USA(-1)) + C(15)*D(L_PIB_USA(-2)) + C(16)*D(L_PIB_USA(-3)) + C(17) |
||||||
| Coeficiente | Error Estándar | Estadístico t | p-valor | |||
| Lp | C(1) | -0.047442667 | 0.01246546 | -3.805929783 | 0.002182614 | |
| Cp | lnXMAT-1 | C(2) | -0.885004777 | 0.270406531 | -3.27286761 | 0.006055765 |
| C(3) | -0.561494936 | 0.343016427 | -1.636933076 | 0.125611021 | ||
| C(4) | -0.671418419 | 0.284154052 | -2.362867654 | 0.034390775 | ||
| lnGIYD | C(5) | -0.150352966 | 0.193898484 | -0.775421048 | 0.451966583 | |
| C(6) | -0.478215311 | 0.230918411 | -2.0709276 | 0.058830949 | ||
| C(7) | -0.28152982 | 0.237962135 | -1.183086627 | 0.257959816 | ||
| lnIED | C(8) | 0.716835533 | 0.207378523 | 3.456652703 | 0.004253456 | |
| C(9) | 0.343275244 | 0.13018569 | 2.636812423 | 0.020519973 | ||
| C(10) | 0.088269422 | 0.079106111 | 1.115835692 | 0.284694034 | ||
| lnIAC | C(11) | 0.052508614 | 0.254270706 | 0.206506739 | 0.839594276 | |
| C(12) | -0.392300517 | 0.285499598 | -1.374084304 | 0.192643773 | ||
| C(13) | -0.13375193 | 0.252743924 | -0.52919939 | 0.605586177 | ||
| lnPIB_USA | C(14) | 1.658497051 | 1.122343785 | 1.477708589 | 0.163300015 | |
| C(15) | 1.223213793 | 1.488485308 | 0.821784257 | 0.426015192 | ||
| C(16) | 2.416068729 | 1.758148932 | 1.374211641 | 0.192605204 | ||
| C | C(17) | 0.108426482 | 0.036351195 | 2.982748757 | 0.010584224 | |
| R2 | 0.747605493 | Media var. dep. | 0.060058931 | |||
| R2 ajustado |
0.436966099 | D.E. var. dep. | 0.100024458 | |||
| E.E. de la regresión | 0.075053937 | Criterio Akaike | -2.044134156 | |||
| Sum Cuad. Res. | 0.073230215 | Criterio Schwarz | -1.250122306 | |||
| Log. Verosimilitud | 47.66201234 | Criterio Hannan-Quinn |
-1.790122943 | |||
| Estadístico F | 2.406666726 | Durbin-Watson | 2.122145555 | |||
| Prob (Estadístico F) | 0.058335441 | |||||
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
En segundo lugar, con base en los datos de la Tabla 7, se aplicó la prueba de Wald con el propósito de evaluar la incidencia de las variables independientes sobre la dependiente en el Cp. Es así como, en la Tabla 8 se puede apreciar que únicamente las variables lnXMAT-1 y lnIED tienen un efecto significativo en la determinación del comportamiento de las XMAT en el Cp.
Dado que las variables utilizadas en el modelo han sido transformadas a logaritmos, los coeficientes estimados representan elasticidades, es decir, miden el cambio porcentual en la variable dependiente ante variaciones porcentuales en las variables independientes. En ese sentido, se observa que el conjunto de variables explicativas (lnXMAT-1, lnGIYD, lnIED, lnIAC y lnPIB_USA) explican el 43.6% de la variación en las exportaciones manufactureras de mediana y alta tecnología en México, de acuerdo con el valor del R2 ajustado. En el Cp, las variables que tienen mayor incidencia sobre el comportamiento de las lnXMAT son su propia dinámica pasada (lnXMAT-1) y las fluctuaciones en la inversión extranjera directa (lnIED). Por su parte, en el Lp, la variabilidad conjunta de las variables independientes determina las alteraciones en este tipo de exportaciones en México (véase Tabla 7 y 8).
Tabla 8. Prueba del Wald
| Variable | Prueba estadística | Valor | df | Probabilidad |
|---|---|---|---|---|
| lnXMAT -1 | Estadístico F | 5.073820 | (3, 13) | 0.0153 |
| Chi-cuadrada | 15.22146 | 3 | 0.0016 | |
| lnGIYD | Estadístico F | 2.122039 | (3, 13) | 0.1467 |
| Chi-cuadrada | 6.366116 | 3 | 0.0951 | |
| lnIED | Estadístico F | 4.663466 | (3, 13) | 0.0201 |
| Chi-cuadrada | 13.99040 | 3 | 0.0029 | |
| lnIAC | Estadístico F | 0.774788 | (3, 13) | 0.5286 |
| Chi-cuadrada | 2.324363 | 3 | 0.5079 | |
| lnPIB_USA | Estadístico F | 0.774788 | (3, 13) | 0.5286 |
| Chi-cuadrada | 2.324363 | 3 | 0.5079 |
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
Las pruebas de validación del modelo indican que los residuales no presentan autocorrelación, son homocedásticos y siguen una distribución normal (véase Tabla 9). Bajo esta misma lógica, el análisis de estabilidad del modelo, realizado a partir de las raíces características del polinomio autorregresivo (AR), revela que los valores mostrados en la Figura 1 son menores a la unidad. Esto implica que no existen problemas de inestabilidad en el modelo y que los residuales pueden considerarse como ruido blanco. En conjunto, estos diagnósticos sugieren que el modelo VECM es adecuado, y que sus estimaciones pueden considerarse insesgadas y eficientes, lo que permite establecer conclusiones válidas.
Tabla 9. Validación del modelo VECM
| Prueba de correlación serial LM: Breusch-Godfrey | |||
|---|---|---|---|
| Estadístico F | 0.2756 | Prob. F(2,11) | 0.7642 |
| Observaciones*R2 | 1.4318 | Prob. Chi-cuadrado(2) | 0.4888 |
| Prueba de Heterocedasticidad: Breusch-Pagan-Godfrey | |||
| Estadístico F | 0.8692 | Prob. F(20,9) | 0.6244 |
| Observaciones*R2 | 19.7664 | Prob. Chi-cuadrado(20) | 0.4726 |
| Escala explicada SS | 1.5250 | Prob. Chi-cuadrado(20) | 1.0000 |
| Jarque-Bera Test: | |||
| Estadístico | 1.7385 | p-valor | 0.4193 |
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
Figura 1. Expresión gráfica del análisis de estabilidad del modelo
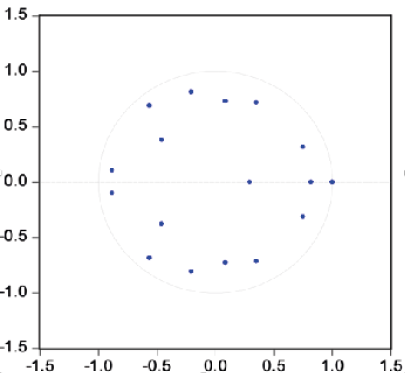
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
La prueba de causalidad de Granger, basada en los resultados del modelo VECM, denotan que existe una relación de causalidad unidireccional de Cp desde el conjunto de variables explicativas hacia la variable dependiente. En particular, se aprecia que la mayor incidencia proviene de los flujos de inversión extranjera directa (lnIED) hacia las exportaciones manufactureras de mediana y alta tecnología (lnXMAT). Esto permite inferir que, en el horizonte de análisis, este tipo de exportaciones continuará en aumento en la medida que lo hagan las variables independientes, especialmente si se incrementa el flujo de IED (véase Tabla 10).
Tabla 10. Prueba de causalidad de Granger.
| Variable dependiente: lnXMAT | |||
|---|---|---|---|
| Variable independiente: | Chi-cuadrada | df | Probabilidad |
| D(lnGIYD) | 6.366115833 | 3 | 0.095094772 |
| D(lnIED) | 13.99039777 | 3 | 0.002918252 |
| D(lnIAC) | 2.324363273 | 3 | 0.507869625 |
| D(lnPIB_USA) | 6.215032166 | 3 | 0.101604453 |
| Todas | 26.22058295 | 12 | 0.009988182 |
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
Tabla 11.. Descomposición de la varianza del error de pronóstico
| Variable dependiente: lnXMAT | ||||||
|---|---|---|---|---|---|---|
| Periodos | Error Estándar | Variables independientes (Variación porcentual) |
||||
| lnXMAT-1 | lnGIYD | lnIED | lnIAC | lnPIB_USA | ||
| 1 | 0.075 | 100.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 0.094 | 73.512 | 0.314 | 14.856 | 10.565 | 0.753 |
| 3 | 0.118 | 50.869 | 0.388 | 28.249 | 18.545 | 1.950 |
| 4 | 0.147 | 39.346 | 3.015 | 26.172 | 28.480 | 2.987 |
| 5 | 0.194 | 44.433 | 1.851 | 18.494 | 25.846 | 9.376 |
| 6 | 0.239 | 48.947 | 1.218 | 14.637 | 21.903 | 13.295 |
| 7 | 0.285 | 51.998 | 0.872 | 12.579 | 19.247 | 15.303 |
| 8 | 0.326 | 53.381 | 0.893 | 11.940 | 17.884 | 15.903 |
| 9 | 0.366 | 53.035 | 1.549 | 10.982 | 17.412 | 17.022 |
| 10 | 0.402 | 53.891 | 1.747 | 10.031 | 16.778 | 17.553 |
Fuente: Elaboración propia con base en datos del BM (2025), y utilizando el paquete estadístico Eviews.
Al contrastar estos resultados con el análisis de descomposición de la varianza, se observa en la Tabla 11 que, en una proyección de cinco años, las variables con mayor incidencia en la dinámica exportadora de bienes manufacturados con contenido medio y alto de tecnología son las experiencias exportadoras previas (lnXMAT-1) y el flujo de inversión extranjera directa (lnIED). Entre los seis y nueve años de proyección, dicha dinámica se verá principalmente influida por la trayectoria exportadora anterior y los procesos de apertura comercial (lnIAC). Finalmente, al cabo de diez años, las exportaciones manufactureras de este tipo estarán determinadas fundamentalmente por las experiencias previas de exportación y la demanda externa (lnPIB_USA).
Discusión de los resultados del modelo VECM
Los resultados del modelo VECM muestran que las exportaciones manufactureras de mediana y alta tecnología en México están determinadas tanto por factores de CP como de LP. En el Cp, destaca el efecto significativo de la variable rezagada de las exportaciones. La literatura atribuye este fenómeno a la acumulación de capacidades, la consolidación de relaciones comerciales y la presencia de costos hundidos de entrada a los mercados internacionales (Navarro et al. 2024; Shahabadi et al., 2023). Así, el desempeño exportador pasado influye en el comportamiento presente, y respalda la necesidad en el caso mexicano de mantener trayectorias de integración comercial estables y sostenidas (Gómez y Camacho, 2011; Güneş et al., 2020).
En este mismo contexto de Cp, se aprecia el efecto positivo de la IED, que actúa como catalizador inmediato al proveer recursos productivos, facilitar la transferencia tecnológica y acelerar la integración a las cadenas globales de valor (Fonkam, 2023; Handoyo et al., 2024). Esta incidencia también se manifiesta en el LP, donde la IED contribuye de forma acumulativa al fortalecimiento de capacidades productivas avanzadas, impulsando sectores manufactureros estratégicos y acrecentando el contenido tecnológico de las exportaciones manufactureras (Cuevas-Ahumada, 2011; Cuevas-Ahumada y Jaime, 2024; Jiménez et al., 2020; Karakostas, 2022; Leogrande et al., 2022). Estos hallazgos evidencian la necesidad de una transformación estructural en México que oriente los beneficios de la IED hacia la generación de derramas tecnológicas, el desarrollo tecnológico propio y la integración de productores nacionales a las cadenas de valor.
Otro factor determinante a LP es el gasto en I+D, el cual tiene una relación directa con la capacidad innovadora del sector y su competitividad en los mercados internacionales (Fayaz y Kaur, 2019; Ríos et al., 2012). Aunque estudios como el Drapkin et al. (2021) señalan que su impacto no es inmediato ni homogéneo. Para la economía mexicana, con limitada inversión pública y privada en I+D, este factor representa una de las principales áreas de oportunidad para el fortalecimiento de las exportaciones manufactureras con contenido tecnológico.
Asimismo, en el Lp la apertura comercial se consolida como un elemento estructural que condiciona el acceso a insumos estratégicos, componentes tecnológicos intermedios y plataformas logísticas internacionales. La literatura señala que las economías con mayor apertura alcanzan altos grados de especialización exportadora y una mejor inserción en las cadenas globales de valor (Anh et al., 2023; Drapkin et al., 2024). Si bien en México la apertura comercial permitió la articulación de un modelo manufacturero exportador, este se basó en la importación de insumos de alta tecnología (Cuevas-Ahumada, 2011; Gómez y Camacho, 2011). Por lo tanto, es necesario el diseño de políticas industriales que acompañen la apertura con aprendizaje tecnológico y eviten la trampa del ensamblaje con bajo contenido nacional.
Finalmente, la demanda externa, específicamente la proveniente de Estados Unidos, reafirma la dependencia estructural del desempeño exportador manufacturero mexicano con respecto a la evolución económica de su principal socio comercial (Frieden, 2007; Reinhart y Rogoff, 2009). Durante eventos disruptivos, como la pandemia de covid-19, se evidencia con claridad esta dependencia, pues ante este suceso se observó una contracción económica sincronizada entre ambos países (Cuevas-Ahumada y Jaime, 2024). Este vínculo remarca la vulnerabilidad del modelo exportador manufacturero mexicano a los choques externos. Por lo tanto, la diversificación de mercados y el fortalecimiento de las capacidades tecnológicas e institucionales deben ser consideradas prioridades estratégicas por atender (Cuevas-Ahumada, 2011; Gómez y Camacho, 2011; Navarro et al. 2024; Shahabadi et al., 2023).
Conclusiones
Los resultados del VECM confirman que las exportaciones manufactureras de media y alta tecnología en México están determinadas por factores tanto de Cp como de LP. En el Cp, el principal impulso proviene del propio desempeño previo de las exportaciones y de los flujos de IED. Estos hallazgos coinciden con la literatura que sostiene que el dinamismo exportador se basa en las capacidades acumuladas y en los procesos de aprendizaje del sector. Asimismo, concuerdan con la literatura que establece que la IED incide en las exportaciones del sector al actuar como un catalizador inmediato, al proveer infraestructura, al promover la integración en redes comerciales y al consolidar la transferencia de tecnología.
En el Lp, el modelo VECM evidencia una relación de equilibrio estable entre las XMAT y sus determinantes estructurales: la XMAT-1, el GIYD, la IED, el IAC, y el PIB_USA. Hallazgos que permiten apreciar que en el Lp la trayectoria exportadora, el gasto en I+D, la IED, la apertura comercial y la demanda externa, especialmente de Estados Unidos, son factores clave para las exportaciones de bienes manufacturas con medio y alto contenido tecnológico, al fortalecer la integración comercial, el desarrollo tecnológico y la inserción en cadenas globales de valor. Asimismo, estos resultados evidencian una dependencia estructural de las exportaciones de México al mercado estadounidense y la necesidad de avanzar hacia una mayor sofisticación productiva en la industria manufacturera mexicana.
En conjunto, a partir de las estimaciones del modelo VECM, se sugiere que la política económica del país aborde de manera integral tanto factores coyunturales como estructurales para fortalecer y acrecentar las exportaciones de bienes tecnológicos. En este sentido, resulta imperativo impulsar decididamente la innovación nacional, fortalecer el desarrollo del capital humano, orientar estratégicamente la IED hacia actividades de mayor valor agregado, complementar la apertura comercial con políticas activas de diversificación, y promover la transformación productiva hacia sectores de mayor complejidad y contenido tecnológico.
Se considera que la presente investigación contribuye significativamente a la literatura existente al proporcionar evidencia actualizada sobre los determinantes de las exportaciones manufactureras de mediana y alta tecnología en México durante el período 1990-2023. A diferencia de estudios previos, se emplea un modelo VECM que permite identificar y diferenciar los efectos de Cp y Lp, incorporando variables que representan diversos factores determinantes de las exportaciones de bienes manufacturados con medio y alto contenido tecnológico. Es así como al adoptar un enfoque híbrido y dinámico, la investigación ofrece una visión más integral del comportamiento de las exportaciones tecnológicas en el contexto de una economía emergente y abierta.
Finalmente, producto del estudio surgen diversas futuras líneas de investigación, como son: el análisis particularizado de cada tipo de exportación tecnológica (alta, mediana y baja), la incorporación al modelo de otro tipo de factores clave para potenciar este tipo de exportaciones manufactureras, la evaluación del impacto de choques externos y eventos extraordinarios, y la realización de análisis comparativos con otros países emergentes o desarrollados. Profundizar en ello permitirá consolidar y ampliar el conocimiento generado por esta investigación, contribuyendo al diseño de políticas públicas más eficaces para promover las exportaciones manufactureras con medio y alto contenido tecnológico en México.